Module 23: Area of Regular Polygons

Claire Elliott

Module 23: Area of Regular Polygons

You may use a calculator throughout this module.

The Pentagon building spans $28.7$ acres ( $116,000\text{ m}^2$ ), and includes an additional $5.1$ acres ( $21,000\text{ m}^2$ ) as a central courtyard.^[1] A pentagon is an example of a regular polygon.

The Pentagon building

A regular polygon has all sides of equal length and all angles of equal measure. Because of this symmetry, a circle can be inscribed—drawn inside the polygon touching each side at one point—or circumscribed—drawn outside the polygon intersecting each vertex. We’ll focus on the inscribed circle first.

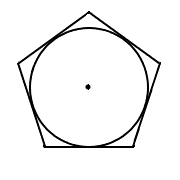
a circle inside a regular pentagon. the circle touches the center of all five sides of the pentagon. — inscribed circle

Let’s call the radius of the inscribed circle lowercase $r$ ; this is the distance from the center of the polygon perpendicular to one of the sides.^[2]

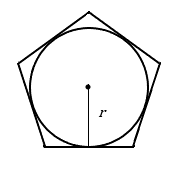
a regular pentagon with a circle inside it touching the center point of each side of the pentagon, and a radius drawn from the center straight down to the center of the bottom side, labeled lowercase r

Area of a Regular Polygon (with a radius drawn to the center of one side)^[3]

For a regular polygon with $n$ sides of length $s$ , and inscribed (inner) radius $r$ ,

$A=nsr\div2$

Note: This formula is derived from dividing the polygon into $n$ equally-sized triangles and combining the areas of those triangles.

Exercises

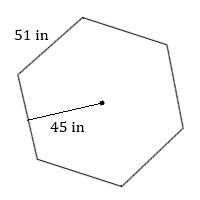
1. Calculate the area of this regular hexagon.

regular hexagon with side 51 in and radius to one side 45 in

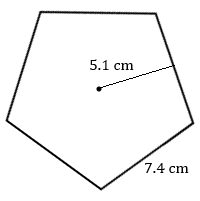
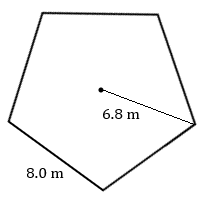
2. Calculate the area of this regular pentagon.

regular pentagon with side 7.4 cm and radius to one side 5.1 cm

3. A stop sign has a a height of $30$ inches, and each edge measures $12.5$ inches. Find the area of the sign.

an octagonal stop sign

Okay, but what if we know the distance from the center to one of the corners instead of the distance from the center to an edge? We’ll need to imagine a circumscribed circle.

a circle outside a regular pentagon. all five corner points of the pentagon touch the circle. — circumscribed circle

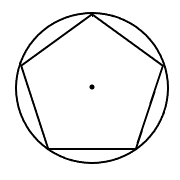
Let’s call the radius of the circumscribed circle capital $R$ ; this is the distance from the center of the polygon to one of the vertices (corners).

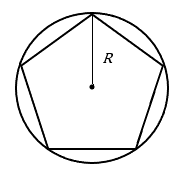
a regular pentagon inside a circle with all five corner points on the circle, and a radius from the center to one corner point labeled capital R

Area of a Regular Polygon (with a radius drawn to a vertex)^[4]

For a regular polygon with $n$ sides of length $s$ , and circumscribed (outer) radius $R$ ,

$A=0.25ns\sqrt{4R^2-s^2}$

or

$A=ns\sqrt{4R^2-s^2}\div4$

Note: This formula is also derived from dividing the polygon into $n$ equally-sized triangles and combining the areas of those triangles. This formula includes a square root because it involves the Pythagorean theorem.

Exercises

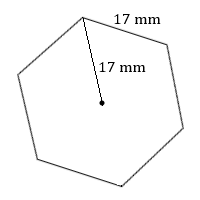
4. Calculate the area of this regular hexagon.

regular hexagon with side 17 mm and radius to one vertex 17 in

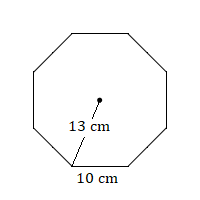
5. Calculate the area of this regular octagon.

octagon with side 10 cm and radius to a vertex 13 cm

6. Calculate the area of this regular pentagon.

regular pentagon with side 8.0 m and radius to one vertex 6.8 m

As you know, a composite figure is a geometric figure which is formed by joining two or more basic geometric figures. Let’s look at a composite figure formed by a circle and a regular polygon.

Exercises

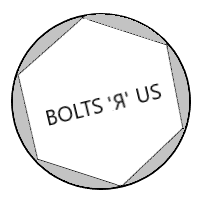
a hexagon labeled "bolts r us" inscribed in a circle

7. The hexagonal head of a bolt fits snugly into a circular cap with a circular hole with inside diameter $46\text{ mm}$ as shown in this diagram. Opposite sides of the bolt head are $40\text{ mm}$ apart. Find the total empty area in the hole around the edges of the bolt head.

https://en.wikipedia.org/wiki/The_Pentagon ↵
The inner radius is more commonly called the apothem and labeled $a$ , but we are trying to keep the jargon to a minimum in this textbook. ↵
This formula is more commonly written as one-half the apothem times the perimeter: $A=\frac{1}{2}ap$ ↵
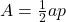Your author created this formula because every other version of it uses trigonometry, which we aren't covering in this textbook. ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

License

Share This Book