Module 12: Percents Part 2 and Error Analysis
You may use a calculator throughout this module.
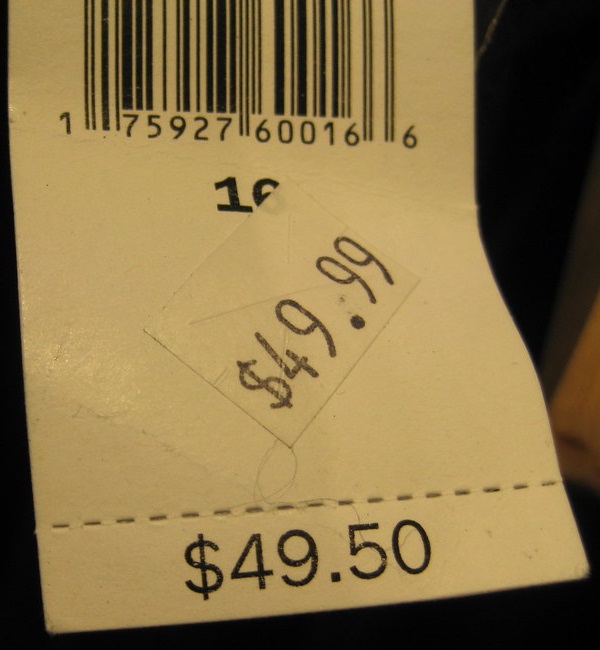 Recall: The amount is the answer we get after finding the percent of the original number. The base is the original number, the number we find the percent of. We can call the percent the rate.
Recall: The amount is the answer we get after finding the percent of the original number. The base is the original number, the number we find the percent of. We can call the percent the rate.
When we looked at percents in a previous module, we focused on finding the amount. In this module, we will learn how to find the percentage rate and the base.
![]()
![]()
We can translate from words into algebra.
- “is” means equals
- “of” means multiply
- “what” means a variable
Solving Percent Problems: Finding the Rate
Suppose you earned ![]() points on a
points on a ![]() -point quiz. To figure out your grade as a percent, you need to answer the question “
-point quiz. To figure out your grade as a percent, you need to answer the question “![]() is what percent of
is what percent of ![]() ?” We can translate this sentence into the equation
?” We can translate this sentence into the equation ![]() .
.
Exercises
1. ![]() is what percent of
is what percent of ![]() ?
?
2. What percent of ![]() is
is ![]() ?
?
Be aware that this method gives us the answer in decimal form and we must move the decimal point to convert the answer to a percent.
Also, if the instructions don’t explicitly tell you how to round your answer, use your best judgment: to the nearest whole percent or nearest tenth of a percent, to two or three significant figures, etc.
Solving Percent Problems: Finding the Base
Suppose you earn ![]() cash rewards for the amount you charge on your credit card. If you want to earn $
cash rewards for the amount you charge on your credit card. If you want to earn $ ![]() in cash rewards, how much do you need to charge on your card? To figure this out, you need to answer the question “
in cash rewards, how much do you need to charge on your card? To figure this out, you need to answer the question “![]() is
is ![]() of what number?” We can translate this into the equation
of what number?” We can translate this into the equation ![]() .
.
Exercises
3. $ ![]() is
is ![]() of what number?
of what number?
4. ![]() of what number is
of what number is ![]() ?
?
Solving Percent Problems: Using Proportions
Recall that a percent is a ratio, a fraction out of ![]() . Instead of translating word for word as we have just been doing, we can set up a proportion with the percentage rate over
. Instead of translating word for word as we have just been doing, we can set up a proportion with the percentage rate over ![]() . Because the base is the original amount, it corresponds to
. Because the base is the original amount, it corresponds to ![]() .
.
Let’s try Exercises 1 through 4 again, using proportions.
Exercises
5. ![]() is what percent of
is what percent of ![]() ?
?
6. What percent of ![]() is
is ![]() ?
?
7. $ ![]() is
is ![]() of what number?
of what number?
8. ![]() of what number is
of what number is ![]() ?
?
Now that we have looked at both methods, you are free to use whichever method you prefer: percent equations or proportions.
Exercises
9. An ![]() tip will be added to a dinner that cost $
tip will be added to a dinner that cost $ ![]() . What is the amount of the tip?
. What is the amount of the tip?
10. The University of Oregon women’s basketball team made ![]() of the
of the ![]() three-points shots they attempted during a game against UNC. What percent of their three-point shots did the team make?
three-points shots they attempted during a game against UNC. What percent of their three-point shots did the team make?
11. ![]() of the people surveyed answered “yes” to a poll question. If
of the people surveyed answered “yes” to a poll question. If ![]() people answered “yes”, how many people were surveyed altogether?
people answered “yes”, how many people were surveyed altogether?
Solving Percent Problems: Percent Increase
When a quantity changes, it is often useful to know by what percent it changed. If the price of a candy bar is increased by ![]() cents, you might be annoyed because it’s it’s a relatively large percentage of the original price. If the price of a car is increased by
cents, you might be annoyed because it’s it’s a relatively large percentage of the original price. If the price of a car is increased by ![]() cents, though, you wouldn’t care because it’s such a small percentage of the original price.
cents, though, you wouldn’t care because it’s such a small percentage of the original price.
To find the percent of increase:
- Subtract the two numbers to find the amount of increase.
- Using this result as the amount and the original number as the base, find the unknown percent.
Notice that we always use the original number for the base, the number that occurred earlier in time. In the case of a percent increase, this is the smaller of the two numbers.
Exercises
12. The price of a candy bar increased from $ ![]() to $
to $ ![]() . By what percent did the price increase?
. By what percent did the price increase?
13. The population of Portland in 2010 was ![]() . The estimated population in 2019 was
. The estimated population in 2019 was ![]() . Find the percent of increase in the population.[1]
. Find the percent of increase in the population.[1]
Solving Percent Problems: Percent Decrease
Finding the percent decrease in a number is very similar.
To find the percent of decrease:
- Subtract the two numbers to find the amount of decrease.
- Using this result as the amount and the original number as the base, find the unknown percent.
Again, we always use the original number for the base, the number that occurred earlier in time. For a percent decrease, this is the larger of the two numbers.
Exercises
14. During a sale, the price of a candy bar was reduced from $ ![]() to $
to $ ![]() . By what percent did the price decrease?
. By what percent did the price decrease?
15. The number of students enrolled at Clackamas Community College decreased from ![]() in Summer 2019 to
in Summer 2019 to ![]() in Summer 2020. Find the percent of decrease in enrollment.
in Summer 2020. Find the percent of decrease in enrollment.
Relative Error
In an earlier module, we said that a measurement will always include some error, no matter how carefully we measure. It can be helpful to consider the size of the error relative to the size of what is being measured. As we saw in the examples above, a difference of ![]() cents is important when we’re pricing candy bars but insignificant when we’re pricing cars. In the same way, an error of an eighth of an inch could be a deal-breaker when you’re trying to fit a screen into a window frame, but an eighth of an inch is insignificant when you’re measuring the length of your garage.
cents is important when we’re pricing candy bars but insignificant when we’re pricing cars. In the same way, an error of an eighth of an inch could be a deal-breaker when you’re trying to fit a screen into a window frame, but an eighth of an inch is insignificant when you’re measuring the length of your garage.
The expected outcome is what the number would be in a perfect world. If a window screen is supposed to be exactly ![]() inches wide, we call this the expected outcome, and we treat it as though it has infinitely many significant digits. In theory, the expected outcome is
inches wide, we call this the expected outcome, and we treat it as though it has infinitely many significant digits. In theory, the expected outcome is ![]()
To find the absolute error, we subtract the measurement and the expected outcome. Because we always treat the expected outcome as though it has unlimited significant figures, the absolute error should have the same precision (place value) as the measurement, not the expected outcome.
To find the relative error, we divide the absolute error by the expected outcome. We usually express the relative error as a percent. In fact, the procedure for finding the relative error is identical to the procedures for finding a percent increase or percent decrease!
To find the relative error:
- Subtract the two numbers to find the absolute error.
- Using the absolute error as the amount and the expected outcome as the base, find the unknown percent.
Exercises
16. A window screen is measured to be ![]() inches wide instead of the advertised
inches wide instead of the advertised ![]() inches. Determine the relative error, rounded to the nearest tenth of a percent.
inches. Determine the relative error, rounded to the nearest tenth of a percent.
17. The contents of a box of cereal are supposed to weigh ![]() ounces, but they are measured at
ounces, but they are measured at ![]() ounces. Determine the relative error, rounded to the nearest tenth of a percent.
ounces. Determine the relative error, rounded to the nearest tenth of a percent.

Tolerance
The tolerance is the maximum amount that a measurement is allowed to differ from the expected outcome. For example, the U.S. Mint needs its coins to have a consistent size and weight so that they will work in vending machines. A dime (10 cents) weighs ![]() grams, with a tolerance of
grams, with a tolerance of ![]() grams.[2] This tells us that the minimum acceptable weight is
grams.[2] This tells us that the minimum acceptable weight is ![]() grams, and the maximum acceptable weight is
grams, and the maximum acceptable weight is ![]() grams. A dime with a weight outside of the range
grams. A dime with a weight outside of the range ![]() would be unacceptable.
would be unacceptable.

Exercises
A U.S. nickel (5 cents) weighs ![]() grams with a tolerance of
grams with a tolerance of ![]() grams.
grams.
18. Determine the lowest acceptable weight and highest acceptable weight of a nickel.
19. Determine the relative error of a nickel that weighs ![]() grams.
grams.
A U.S. quarter (25 cents) weighs ![]() grams with a tolerance of
grams with a tolerance of ![]() grams.
grams.
20. Determine the lowest acceptable weight and highest acceptable weight of a quarter.
21. Determine the relative error of a quarter that weighs ![]() grams.
grams.

