Module 40: Use the Rectangular Coordinate System
Learning Objectives
By the end of this section, you will be able to:
- Plot points in a rectangular coordinate system
- Verify solutions to an equation in two variables
- Complete a table of solutions to a linear equation
- Find solutions to a linear equation in two variables
Plot Points on a Rectangular Coordinate System
Just like maps use a grid system to identify locations, a grid system is used in algebra to show a relationship between two variables in a rectangular coordinate system. The rectangular coordinate system is also called the xy-plane or the ‘coordinate plane.’
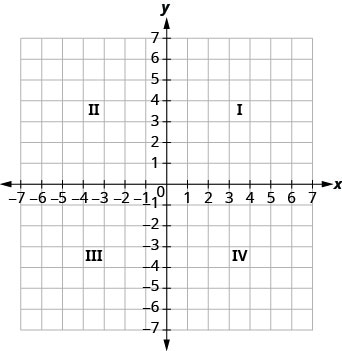
The horizontal number line is called the x-axis. The vertical number line is called the y-axis. The x-axis and the y-axis together form the rectangular coordinate system. These axes divide a plane into four regions, called quadrants. The quadrants are identified by Roman numerals, beginning on the upper right and proceeding counterclockwise. See (Figure 1).
‘Quadrant’ has the root ‘quad,’ which means ‘four.’
In the rectangular coordinate system, every point is represented by an ordered pair. The first number in the ordered pair is the x-coordinate of the point, and the second number is the y-coordinate of the point.
Ordered pair
An ordered pair, ![]() , gives the coordinates of a point in a rectangular coordinate system.
, gives the coordinates of a point in a rectangular coordinate system.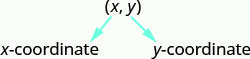
The first number is the x-coordinate.
The second number is the y-coordinate.
The phrase ‘ordered pair’ means the order is important. What is the ordered pair of the point where the axes cross? At that point both coordinates are zero, so its ordered pair is ![]() . The point
. The point ![]() has a special name. It is called the origin.
has a special name. It is called the origin.
The origin
The point ![]() is called the origin. It is the point where the x-axis and y-axis intersect.
is called the origin. It is the point where the x-axis and y-axis intersect.
We use the coordinates to locate a point on the xy-plane. Let’s plot the point ![]() as an example. First, locate 1 on the x-axis and lightly sketch a vertical line through
as an example. First, locate 1 on the x-axis and lightly sketch a vertical line through ![]() . Then, locate 3 on the y-axis and sketch a horizontal line through
. Then, locate 3 on the y-axis and sketch a horizontal line through ![]() . Now, find the point where these two lines meet—that is the point with coordinates
. Now, find the point where these two lines meet—that is the point with coordinates ![]() .
.
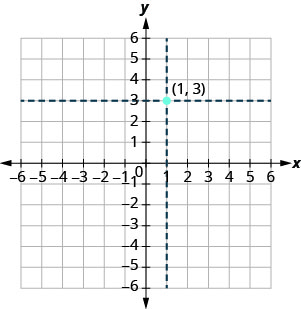
Notice that the vertical line through ![]() and the horizontal line through
and the horizontal line through ![]() are not part of the graph. We just used them to help us locate the point
are not part of the graph. We just used them to help us locate the point ![]() .
.
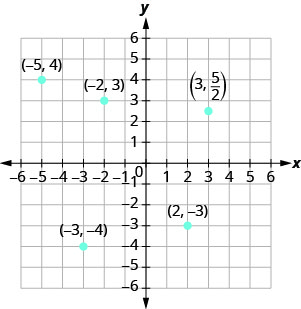
EXAMPLE 1
Plot each point in the rectangular coordinate system and identify the quadrant in which the point is located:
A ![]() B
B ![]() C
C ![]() D
D ![]() E
E ![]() .
.
Solution
The first number of the coordinate pair is the x-coordinate, and the second number is the y-coordinate.
- Since
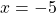 , the point is to the left of the y-axis. Also, since
, the point is to the left of the y-axis. Also, since 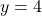 , the point is above the x-axis. The point
, the point is above the x-axis. The point 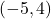 is in Quadrant II.
is in Quadrant II. - Since
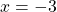 , the point is to the left of the y-axis. Also, since
, the point is to the left of the y-axis. Also, since 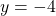 , the point is below the x-axis. The point
, the point is below the x-axis. The point 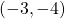 is in Quadrant III.
is in Quadrant III. - Since
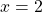 , the point is to the right of the y-axis. Since
, the point is to the right of the y-axis. Since 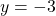 , the point is below the x-axis. The point
, the point is below the x-axis. The point 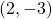 is in Quadrant lV.
is in Quadrant lV. - Since
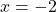 , the point is to the left of the y-axis. Since
, the point is to the left of the y-axis. Since 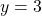 , the point is above the x-axis. The point
, the point is above the x-axis. The point 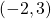 is in Quadrant II.
is in Quadrant II. - Since
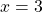 , the point is to the right of the y-axis. Since
, the point is to the right of the y-axis. Since 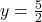 , the point is above the x-axis. (It may be helpful to write
, the point is above the x-axis. (It may be helpful to write 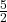 as a mixed number or decimal.) The point
as a mixed number or decimal.) The point 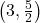 is in Quadrant I.
is in Quadrant I.
TRY IT 1.1
Plot each point in a rectangular coordinate system and identify the quadrant in which the point is located:
A ![]() B
B ![]() C
C ![]() D
D ![]() E
E ![]() .
.
Show answer
TRY IT 1.2
Plot each point in a rectangular coordinate system and identify the quadrant in which the point is located:
A ![]() B
B ![]() C
C ![]() D
D ![]() E
E ![]()
Show answer
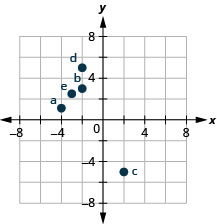
How do the signs affect the location of the points? You may have noticed some patterns as you graphed the points in the previous example.
For the point in (Figure 2) in Quadrant IV, what do you notice about the signs of the coordinates? What about the signs of the coordinates of points in the third quadrant? The second quadrant? The first quadrant?
Can you tell just by looking at the coordinates in which quadrant the point ![]() is located? In which quadrant is
is located? In which quadrant is ![]() located?
located?
Quadrants
We can summarize sign patterns of the quadrants in this way.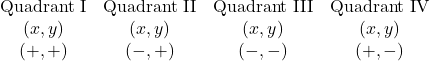
What if one coordinate is zero as shown in (Figure 3)? Where is the point ![]() located? Where is the point
located? Where is the point ![]() located?
located?
The point ![]() is on the y-axis and the point
is on the y-axis and the point ![]() is on the x-axis.
is on the x-axis.
Points on the axes
Points with a y-coordinate equal to 0 are on the x-axis, and have coordinates ![]() .
.
Points with an x-coordinate equal to 0 are on the y-axis, and have coordinates ![]() .
.
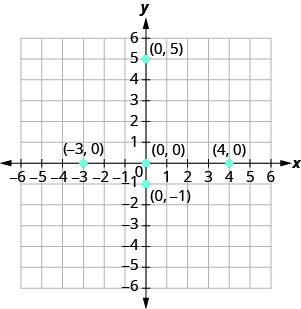
EXAMPLE 2
Plot each point:A ![]() B
B ![]() C
C ![]() D
D ![]() E
E ![]() .
.
Solution
- Since
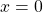 , the point whose coordinates are
, the point whose coordinates are 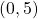 is on the y-axis.
is on the y-axis. - Since
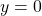 , the point whose coordinates are
, the point whose coordinates are 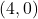 is on the x-axis.
is on the x-axis. - Since
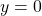 , the point whose coordinates are
, the point whose coordinates are 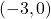 is on the x-axis.
is on the x-axis. - Since
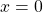 and
and 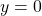 , the point whose coordinates are
, the point whose coordinates are 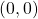 is the origin.
is the origin. - Since
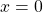 , the point whose coordinates are
, the point whose coordinates are  is on the y-axis.
is on the y-axis.
TRY IT 2.1
Plot each point: A ![]() B
B ![]() C
C ![]() D
D ![]() E
E ![]() .
.
Show answer
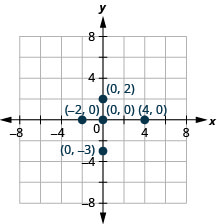
TRY IT 2.2
Plot each point: A ![]() B
B ![]() C
C ![]() D
D ![]() E
E ![]() .
.
Show answer
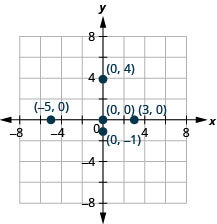
In algebra, being able to identify the coordinates of a point shown on a graph is just as important as being able to plot points. To identify the x-coordinate of a point on a graph, read the number on the x-axis directly above or below the point. To identify the y-coordinate of a point, read the number on the y-axis directly to the left or right of the point. Remember, when you write the ordered pair use the correct order, ![]() .
.
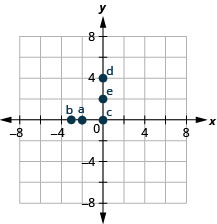
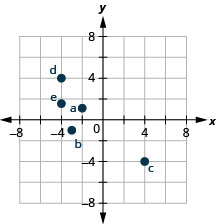
EXAMPLE 3
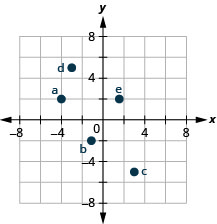
Name the ordered pair of each point shown in the rectangular coordinate system.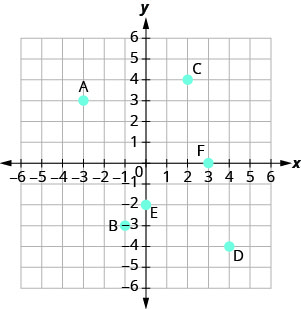
Solution
Point A is above ![]() on the x-axis, so the x-coordinate of the point is
on the x-axis, so the x-coordinate of the point is ![]() .
.
- The point is to the left of 3 on the y-axis, so the y-coordinate of the point is 3.
- The coordinates of the point are
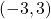 .
.
Point B is below ![]() on the x-axis, so the x-coordinate of the point is
on the x-axis, so the x-coordinate of the point is ![]() .
.
- The point is to the left of
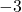 on the y-axis, so the y-coordinate of the point is
on the y-axis, so the y-coordinate of the point is 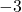 .
. - The coordinates of the point are
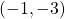 .
.
Point C is above 2 on the x-axis, so the x-coordinate of the point is 2
- The point is to the right of 4 on the y-axis, so the y-coordinate of the point is 4.
- The coordinates of the point are
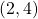 .
.
Point D is below 4 on the x-axis, so the x-coordinate of the point is 4
- The point is to the right of
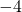 on the y-axis, so the y-coordinate of the point is
on the y-axis, so the y-coordinate of the point is 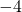 .
. - The coordinates of the point are
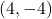 .
.
Point E is on the y-axis at ![]() . The coordinates of point E are
. The coordinates of point E are ![]() .
.
Point F is on the x-axis at ![]() . The coordinates of point F are
. The coordinates of point F are ![]() .
.
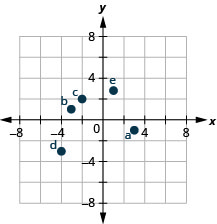
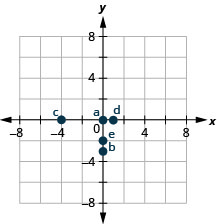
TRY IT 3.1
Name the ordered pair of each point shown in the rectangular coordinate system. 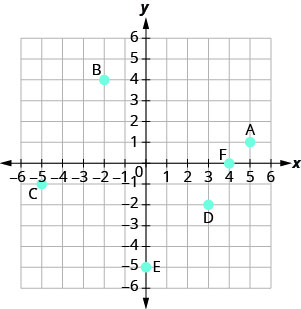
Show answer
A: ![]() B:
B: ![]() C:
C: ![]() D:
D: ![]() E:
E: ![]() F:
F: ![]()
TRY IT 3.2
Name the ordered pair of each point shown in the rectangular coordinate system. 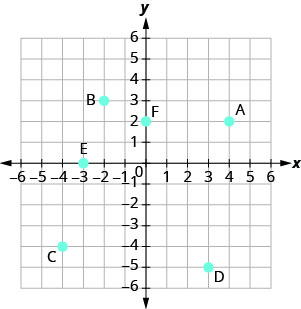
Show answer
A: ![]() B:
B: ![]() C:
C: ![]() D:
D: ![]() E:
E: ![]() F:
F: ![]()
Verify Solutions to an Equation in Two Variables
Up to now, all the equations you have solved were equations with just one variable. In almost every case, when you solved the equation you got exactly one solution. The process of solving an equation ended with a statement like ![]() . (Then, you checked the solution by substituting back into the equation.)
. (Then, you checked the solution by substituting back into the equation.)
Here’s an example of an equation in one variable, and its one solution.
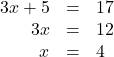
But equations can have more than one variable. Equations with two variables may be of the form ![]() . Equations of this form are called linear equations in two variables.
. Equations of this form are called linear equations in two variables.
Linear equation
An equation of the form ![]() , where
, where ![]() and
and ![]() are not both zero, is called a linear equation in two variables.
are not both zero, is called a linear equation in two variables.
Notice the word line in linear. Here is an example of a linear equation in two variables, ![]() and
and ![]() .
.
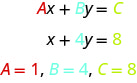
The equation ![]() is also a linear equation. But it does not appear to be in the form
is also a linear equation. But it does not appear to be in the form ![]() . We can use the Addition Property of Equality and rewrite it in
. We can use the Addition Property of Equality and rewrite it in ![]() form.
form.
| Add to both sides. | |
| Simplify. | |
| Use the Commutative Property to put it in |
By rewriting ![]() as
as ![]() , we can easily see that it is a linear equation in two variables because it is of the form
, we can easily see that it is a linear equation in two variables because it is of the form ![]() . When an equation is in the form
. When an equation is in the form ![]() , we say it is in standard form.
, we say it is in standard form.
Standard Form of Linear Equation
A linear equation is in standard form when it is written ![]() .
.
Most people prefer to have ![]() ,
, ![]() , and
, and ![]() be integers and
be integers and ![]() when writing a linear equation in standard form, although it is not strictly necessary.
when writing a linear equation in standard form, although it is not strictly necessary.
Linear equations have infinitely many solutions. For every number that is substituted for ![]() there is a corresponding
there is a corresponding ![]() value. This pair of values is a solution to the linear equation and is represented by the ordered pair
value. This pair of values is a solution to the linear equation and is represented by the ordered pair ![]() . When we substitute these values of
. When we substitute these values of ![]() and
and ![]() into the equation, the result is a true statement, because the value on the left side is equal to the value on the right side.
into the equation, the result is a true statement, because the value on the left side is equal to the value on the right side.
Solution of a Linear Equation in Two Variables
An ordered pair ![]() is a solution of the linear equation
is a solution of the linear equation ![]() , if the equation is a true statement when the x– and y-values of the ordered pair are substituted into the equation.
, if the equation is a true statement when the x– and y-values of the ordered pair are substituted into the equation.
EXAMPLE 4
Determine which ordered pairs are solutions to the equation ![]() .
.
A ![]() B
B ![]() C
C ![]()
Solution
Substitute the x- and y-values from each ordered pair into the equation and determine if the result is a true statement.

TRY IT 4.1
Which of the following ordered pairs are solutions to ![]() ?
?
A ![]() B
B ![]() C
C ![]()
Show answer
A, C
TRY IT 4.2
Which of the following ordered pairs are solutions to the equation ![]() ? A
? A ![]() B
B ![]() C
C ![]()
Show answer
B, C
EXAMPLE 5
Which of the following ordered pairs are solutions to the equation ![]() ?
?
A ![]() B
B ![]() C
C ![]()
Solution
Substitute the x– and y-values from each ordered pair into the equation and determine if it results in a true statement.
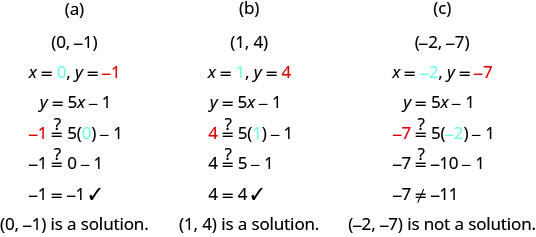
TRY IT 5.1
Which of the following ordered pairs are solutions to the equation ![]() ? A
? A ![]() B
B ![]() C
C ![]()
Show answer
B
TRY IT 5.2
Which of the following ordered pairs are solutions to the equation ![]() ? A
? A ![]() B
B ![]() C
C ![]()
Show answer
A, B
Complete a Table of Solutions to a Linear Equation in Two Variables
In the examples above, we substituted the x– and y-values of a given ordered pair to determine whether or not it was a solution to a linear equation. But how do you find the ordered pairs if they are not given? It’s easier than you might think—you can just pick a value for ![]() and then solve the equation for
and then solve the equation for ![]() . Or, pick a value for
. Or, pick a value for ![]() and then solve for
and then solve for ![]() .
.
We’ll start by looking at the solutions to the equation ![]() that we found in (Example 5). We can summarize this information in a table of solutions, as shown in (Table 1).
that we found in (Example 5). We can summarize this information in a table of solutions, as shown in (Table 1).
| 0 | ||
| 1 | 4 | |
To find a third solution, we’ll let ![]() and solve for
and solve for ![]() .
.
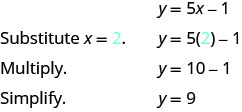
The ordered pair ![]() is a solution to
is a solution to ![]() . We will add it to (Table 2).
. We will add it to (Table 2).
| 0 | ||
| 1 | 4 | |
| 2 | 9 | |
We can find more solutions to the equation by substituting in any value of ![]() or any value of
or any value of ![]() and solving the resulting equation to get another ordered pair that is a solution. There are infinitely many solutions of this equation.
and solving the resulting equation to get another ordered pair that is a solution. There are infinitely many solutions of this equation.
EXAMPLE 6
Complete the table to find three solutions to the equation ![]() .
.
| 0 | ||
| 2 | ||
Substitute ![]() ,
, ![]() , and
, and ![]() into
into ![]() .
.
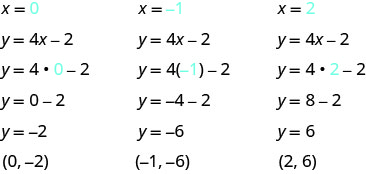
The results are summarized in the table below.
| 0 | ||
| 2 | 6 | |
TRY IT 6.1
Complete the table to find three solutions to this equation: ![]() .
.
| 0 | ||
| 2 | ||
Show answer
| 0 | ||
| 2 | 5 | |
TRY IT 6.2
Complete the table to find three solutions to this equation: ![]() .
.
| 0 | ||
| 1 | ||
Show answer
| 0 | 1 | |
| 1 | 7 | |
EXAMPLE 7
Complete the table to find three solutions to the equation ![]() .
.
| 0 | ||
| 0 | ||
| 5 | ||
Substitute the given value into the equation ![]() and solve for the other variable. Then, fill in the values in the table.
and solve for the other variable. Then, fill in the values in the table.
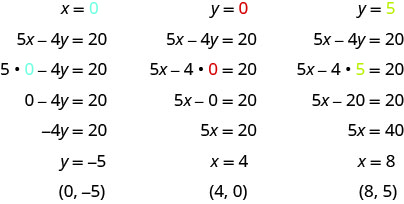
The results are summarized in the table below.
| 0 | ||
| 4 | 0 | |
| 8 | 5 | |
TRY IT 7.1
Complete the table to find three solutions to this equation: ![]() .
.
| 0 | ||
| 0 | ||
Show answer
| 0 | ||
| 10 | 0 | |
TRY IT 7.2
Complete the table to find three solutions to this equation: ![]() .
.
| 0 | ||
| 0 | ||
Show answer
| 0 | ||
| 4 | 0 | |
Find Solutions to a Linear Equation
To find a solution to a linear equation, you really can pick any number you want to substitute into the equation for ![]() or
or ![]() . But since you’ll need to use that number to solve for the other variable it’s a good idea to choose a number that’s easy to work with.
. But since you’ll need to use that number to solve for the other variable it’s a good idea to choose a number that’s easy to work with.
When the equation is in y-form, with the y by itself on one side of the equation, it is usually easier to choose values of ![]() and then solve for
and then solve for ![]() .
.
EXAMPLE 8
Find three solutions to the equation ![]() .
.
We can substitute any value we want for ![]() or any value for
or any value for ![]() . Since the equation is in y-form, it will be easier to substitute in values of
. Since the equation is in y-form, it will be easier to substitute in values of ![]() . Let’s pick
. Let’s pick ![]() ,
, ![]() , and
, and ![]() .
.
 |
 |
 |
|||
| Substitute the value into the equation. | 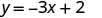 |
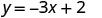 |
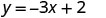 |
||
| Simplify. | 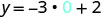 |
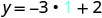 |
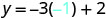 |
||
| Simplify. | 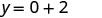 |
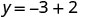 |
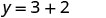 |
||
| Write the ordered pair. |  |
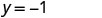 |
 |
||
| Check. | (0, 2) | (1, −1) | (−1, 5) | ||
So, ![]() ,
, ![]() and
and ![]() are all solutions to
are all solutions to ![]() . We show them in table below.
. We show them in table below.
| 0 | 2 | |
| 1 | ||
| 5 | ||
TRY IT 8.1
Find three solutions to this equation: ![]() .
.
Show answer
Answers will vary.
TRY IT 8.2
Find three solutions to this equation: ![]() .
.
Show answer
Answers will vary
We have seen how using zero as one value of ![]() makes finding the value of
makes finding the value of ![]() easy. When an equation is in standard form, with both the
easy. When an equation is in standard form, with both the ![]() and
and ![]() on the same side of the equation, it is usually easier to first find one solution when
on the same side of the equation, it is usually easier to first find one solution when ![]() find a second solution when
find a second solution when ![]() , and then find a third solution.
, and then find a third solution.
EXAMPLE 9
Find three solutions to the equation ![]() .
.
We can substitute any value we want for ![]() or any value for
or any value for ![]() . Since the equation is in standard form, let’s pick first
. Since the equation is in standard form, let’s pick first ![]() , then
, then ![]() , and then find a third point.
, and then find a third point.
 |
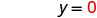 |
 |
|||
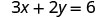 |
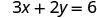 |
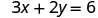 |
|||
| Substitute the value into the equation. | 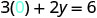 |
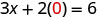 |
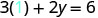 |
||
| Simplify. | 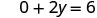 |
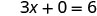 |
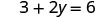 |
||
| Solve. | 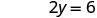 |
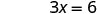 |
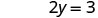 |
||
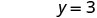 |
 |
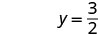 |
|||
| Write the ordered pair. | (0, 3) | (2, 0) | |||
| Check. | |||||
So ![]() ,
, ![]() , and
, and ![]() are all solutions to the equation
are all solutions to the equation ![]() . We can list these three solutions in the table below.
. We can list these three solutions in the table below.
| 0 | 3 | |
| 2 | 0 | |
| 1 | ||
EXAMPLE 9.1
Find three solutions to the equation ![]() .
.
Show answer
Answers will vary.
TRY IT 9.2
Find three solutions to the equation ![]() .
.
Show answer
Answers will vary.
Glossary
- linear equation
- A linear equation is of the form
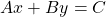 , where A and B are not both zero, is called a linear equation in two variables.
, where A and B are not both zero, is called a linear equation in two variables.
- ordered pair
- An ordered pair
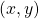 gives the coordinates of a point in a rectangular coordinate system.
gives the coordinates of a point in a rectangular coordinate system.
- origin
- The point
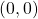 is called the origin. It is the point where the x-axis and y-axis intersect.
is called the origin. It is the point where the x-axis and y-axis intersect.
- quadrant
- The x-axis and the y-axis divide a plane into four regions, called quadrants.
- rectangular coordinate system
- A grid system is used in algebra to show a relationship between two variables; also called the xy-plane or the ‘coordinate plane.’
- x-coordinate
- The first number in an ordered pair
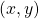 .
.
- y-coordinate
- The second number in an ordered pair
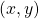 .
.
Practice Exercises
Exercises
Plot Points in a Rectangular Coordinate System
In the following exercises, plot each point in a rectangular coordinate system and identify the quadrant in which the point is located.
|
1.A |
2. A B C D E |
| 3. A B C D E |
4. A B C D E |
In the following exercises, plot each point in a rectangular coordinate system.
| 5. A B C D E |
6. A B C D E |
| 7. A B C D E |
8. A B C D E |
In the following exercises, name the ordered pair of each point shown in the rectangular coordinate system.
9.
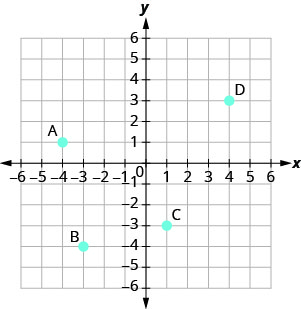 |
10. 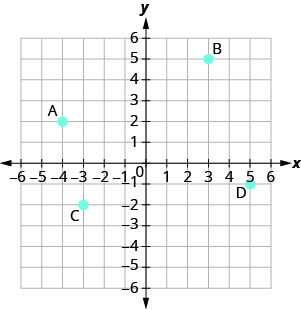 |
|
11.
 |
12. 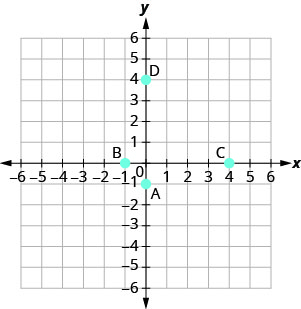 |
Exercises
Verify Solutions to an Equation in Two Variables
In the following exercises, which ordered pairs are solutions to the given equations?
| 13. A |
14. A |
|
15. A |
16. A |
|
17. A |
18. A |
|
19. A |
20. A |
Complete a Table of Solutions to a Linear Equation
In the following exercises, complete the table to find solutions to each linear equation.
21.
|
22.
|
||||||||||||||||||||||||
|
23.
|
24.
|
||||||||||||||||||||||||
|
25.
|
26.
|
||||||||||||||||||||||||
|
27.
|
28.
|
||||||||||||||||||||||||
|
29.
|
30.
|
||||||||||||||||||||||||
|
31.
|
32.
|
Find Solutions to a Linear Equation
In the following exercises, find three solutions to each linear equation.
| 33. |
34. |
| 35. |
36. |
| 37. |
38. |
| 39. |
40. |
| 41. |
42. |
| 43. |
44. |
| 45. |
46. |
| 47. |
48. |
Exercises
Everyday Math
|
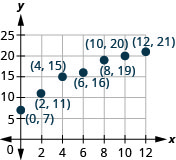
49. Weight of a baby. Mackenzie recorded her baby’s weight every two months. The baby’s age, in months, and weight, in pounds, are listed in the table below, and shown as an ordered pair in the third column. a) Plot the points on a coordinate plane.
b) Why is only Quadrant I needed?
|
50. Weight of a child. Latresha recorded her son’s height and weight every year. His height, in inches, and weight, in pounds, are listed in the table below, and shown as an ordered pair in the third column. a) Plot the points on a coordinate plane.
b) Why is only Quadrant I needed?
|
Writing Exercises
| 51. Explain in words how you plot the point |
52. How do you determine if an ordered pair is a solution to a given equation? |
| 53. Is the point |
54. Is the point |
Answers
| 1.
|
3.
|
||||||||||||||||||||||||
| 5.
|
7.
|
||||||||||||||||||||||||
| 9. A: |
11. A: |
||||||||||||||||||||||||
| 13. A, B | 15. A, C | ||||||||||||||||||||||||
| 17. B, C | 19. A, B | ||||||||||||||||||||||||
21.
|
23.
|
||||||||||||||||||||||||
25.
|
25.
|
||||||||||||||||||||||||
27.
|
29.
|
||||||||||||||||||||||||
31.
|
33. Answers will vary. | ||||||||||||||||||||||||
| 35. Answers will vary. | 37. Answers will vary. | ||||||||||||||||||||||||
| 39. Answers will vary. | 41. Answers will vary. | ||||||||||||||||||||||||
| 43. Answers will vary. | 45. Answers will vary. | ||||||||||||||||||||||||
| 47. Answers will vary. | 49.
a)
b) Age and weight are only positive. |
||||||||||||||||||||||||
| 51. Answers will vary. | 53. Answers will vary. |
Attributions
This chapter has been adapted from “Use the Rectangular Coordinate System” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence. Adapted by Izabela Mazur. See the Copyright page for more information.