"

34 9.2 Measures of Association

[latexpage]

Besides looking at the scatter plot and seeing that a linear relationship seems reasonable, and identifying a positive or negative trend, how can you tell more about this relationship?  While it is always good practice to first examine things visually, you may find that deciphering a scatterplot, especially the strength of a relationship can be tricky.  The next step is then to then calculate numerical measures of this association.

The Correlation Coefficient, r

The correlation coefficient, r, developed by Karl Pearson in the early 1900s, is a numerical measure that provides a measure of strength and direction of the linear association between the independent variable x and the dependent variable y.

The correlation coefficient can be calculated using the formula:

\(r=\frac{n\Sigma \left(xy\right)-\left(\Sigma x\right)\left(\Sigma y\right)}{\sqrt{\left[n\Sigma {x}^{2}-{\left(\Sigma x\right)}^{2}\right]\left[n\Sigma {y}^{2}-{\left(\Sigma y\right)}^{2}\right]}}\)

where n = the number of data points.

The formula for r is formidable, so I would not recommend doing this by hand, however technology can make quick work of the calculation.

If you suspect a linear relationship between x and y, then r can measure how strong the linear relationship is.

What the VALUE of r tells us:

  • The value of r is always between –1 and +1: –1 ≤ r ≤ 1.
  • The size of the correlation r indicates the strength of the linear relationship between x and y. Values of r close to –1 or to +1 indicate a stronger linear relationship between x and y.
  • If r = 0 there is likely no linear correlation. It is important to view the scatterplot, however, because data that exhibit a curved or horizontal pattern may have a correlation of 0.
  • If r = 1, there is perfect positive correlation. If r = –1, there is perfect negative correlation. In both these cases, all of the original data points lie on a straight line. Of course, in the real world, this will not generally happen.

What the SIGN of r tells us

  • A positive value of r means that when x increases, y tends to increase and when x decreases, y tends to decrease (positive correlation).
  • A negative value of r means that when x increases, y tends to decrease and when x decreases, y tends to increase (negative correlation).
  • The sign of r is the same as the sign of the slope, b, of the best-fit line.
Note: Strong correlation does not suggest that x causes y or y causes x. We say “correlation does not imply causation.”

Example

A random sample of 11 statistics students produced the following data, where x is the third exam score out of 80, and y is the final exam score out of 200.

Figure 9.7: Third and Final Exam Scores Data
x (third exam score) y (final exam score)
65 175
67 133
71 185
71 163
66 126
75 198
67 153
70 163
71 159
69 151
69 159
A scatter plot showing the scores on the final exam based on scores from the third exam is a follows.
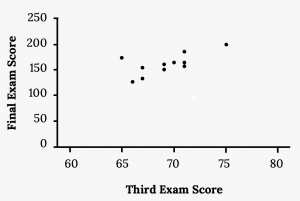
Scatter plot of the data provided. The third exam score is plotted on the x-axis, and the final exam score is plotted on the y-axis. The points form a strong, positive, linear pattern.
Figure 9.8: Third and Final Exam Scores Scatterplot

Find the correlation coefficient:

Your turn!

Match the following scatter plots with their description of correlation coefficient

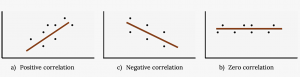
Three scatter plots with lines of best fit. The first scatterplot shows points ascending from the lower left to the upper right. The line of best fit has positive slope. The second scatter plot shows points descending from the upper left to the lower right. The line of best fit has negative slope. The third scatter plot of points form a horizontal pattern. The line of best fit is a horizontal line.
Figure 9.9: Matching Scatterplots to Correlation Coefficients
  1. –1 < r < 0
  2. r = 0
  3. 0 < r < 1

The Coefficient of Determination, r2

The coefficient of determination, r2 , is (obviously) the square of the correlation coefficient, but is usually stated as a percent, rather than in decimal form. It has an interpretation in the context of the data:

  • \({r}^{2}\), when expressed as a percent, represents the percent of variation in the dependent (predicted) variable y that can be explained by variation in the independent (explanatory) variable x using the regression (best-fit) line.
  • 1 – \({r}^{2}\), when expressed as a percentage, represents the percent of variation in y that is NOT explained by variation in x using the regression line. This can be seen as the scattering of the observed data points about the regression line.

Example

Recall our previous example using a student’s third exam scores to predict their final exam scores:

We found the correlation coefficient is r = 0.6631.

Find the coefficient of determination:

Interpret of r2 in the context of this example:

Image References

Figure 9.8: Kindred Grey via Virginia Tech (2020). “Figure 9.8” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_9.8.png . Adaptation of Figure 12.9 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/12-3-the-regression-equation

Figure 9.9: Kindred Grey via Virginia Tech (2020). “Figure 9.9” CC BY-SA 4.0. Retrieved from https://commons.wikimedia.org/wiki/File:Figure_9.9.png . Adaptation of Figure 12.13 from OpenStax Introductory Statistics (2013) (CC BY 4.0). Retrieved from https://openstax.org/books/introductory-statistics/pages/12-3-the-regression-equation

definition

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Significant Statistics Copyright © 2020 by John Morgan Russell, OpenStaxCollege, OpenIntro is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book