Exponents and Scientific Notation: Workbook Examples/Practice

jtrude

4 Exponents and Scientific Notation: Workbook Examples/Practice

6.1 Working With Exponents

Exponents often can be simplified using a few basic properties, since exponents represent repeated multiplication. The basic structure of writing an exponent looks like $x^y,$ where $x$ is defined as the base and $y$ is termed its exponent. For this instance, $y$ represents the number of times that the variable $x$ is multiplied by itself.

Once there is an exponent as a base that is multiplied or divided by itself to the number represented by the exponent, it becomes straightforward to identify a number of rules and properties that can be defined.

The following examples outline a number of these rules.

6.1 Examples/Practice

Simplify the following.

1.) $4\cdot 4^4\cdot 4^2$

2.) $2m^4n^2\cdot 4nm^2$

3.) $x^2y^4\cdot xy^2$

4.) $(3^3)^4$

5.) $(2u^3v^2)^2$

6.) $(xy)^3$

7.) $4^5 \div 4^3$

8.) $x^2y^4 \div 4xy$

9.) $[(2x)^3 \div x^3]^2$

Summary of the Rules of Exponents

$\text{Product Rule of Exponents: }x^m \times x^n = x^{m+n}$

$\text{Power of a Power Rule of Exponents: }(x^m)^n = x^{mn}$

$\text{Power of a Product Rule of Exponents: }(xy)^n = x^ny^n$

$\text{Quotient Rule of Exponents: }\dfrac{x^m}{x^n}=x^{m-n}\hspace{0.25in} (x \ne 0)$

$\text{Power of a Quotient Rule of Exponents: }\left(\dfrac{x}{y}\right)^n = \dfrac{x^n}{y^n}\hspace{0.25in} (y \ne 0)$

6.2 Negative Exponents

Consider the following chart that shows the expansion of $a$ for several exponents:

$\begin{array}{lllllllll} a^3&=&a&\times &a&\times &a&& \\ a^2&=&a&\times &a&&&& \\ \end{array}$

$\begin{array}{lll} a^{-1}&=&\dfrac{1}{a} \\ \\ a^{-2}&=&\dfrac{1}{(a\times a)} \\ \\ a^{-3}&=&\dfrac{1}{(a\times a\times a)} \\ \\ a^{-4}&=&\dfrac{1}{(a\times a\times a\times a)} \end{array}$

If zero and negative exponents are expanded to base 2, the result is the following:

$\begin{array}{llcll} 2^0&=&1&& \\ \\ 2^{-1}&=&\dfrac{1}{2}&& \\ \\ 2^{-2}&=&\dfrac{1}{2\times 2}&\text{or}&\dfrac{1}{4} \\ \\ \end{array}$

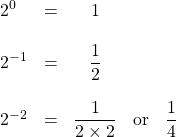
The most unusual of these is the exponent 0. Any base that is not equal to zero to the zeroth exponent is always 1. The simplest explanation of this is by example.

Simplify $\dfrac{x^2}{x^2}$ .

Using the quotient rule of exponents, we know that this simplifies to $x^{2-2}$ , which equals $x^0.$ And we know

$\dfrac{2^2}{2^2} = \dfrac{4}{4}=1$ ,

When dealing with negative exponents, the simplest solution is to reciprocate the power.

Simplify $3x^{-2}y^2$
Since the only negative exponent is $x^{-2}$ , this simplifies to $\dfrac{3y^2}{x^2}.$

6.2 Examples/Practice

Simplify. Your answer should contain only positive exponents.

1.) $(2x^4y^{-2})(2xy^3)^4$

2.) $(2a^{-2}b^{-3})(2a^0b^4)^4$

3.) $(2x^2y^2)^4x^{-4}$

4.) $[(m^0n^3)(2m^{-3}n^{-3})]^0$

5.) $(2x^{-3}y^2)\div (3x^{-3}y^3\cdot 3x^0)$

6.) $3y^3\div [(3yx^3)(2x^4y^{-3})]$

7.) $2y\div (x^0y^2)^4$

8.) $(a^4)^4\div 2b$

Summary of the Rules of Zero Exponent and Negative Exponents

$\text{Zero Power Rule of Exponents: }x^0 = 1\hspace{0.25in} (x \ne 0)$

$x^{-n}=\dfrac{1}{x^n}\hspace{0.25in} (x \ne 0)$

$\dfrac{1}{x^{-n}}=x^n\hspace{0.25in} (x \ne 0)$

$\left(\dfrac{x}{y}\right)^{-n}=\left(\dfrac{y}{x}\right)^n \hspace{0.25in} (x,y \ne 0)$

$\left(\dfrac{x^ay^b}{z^c}\right)^{-n}=\dfrac{z^{cn}}{x^{an}y^{bn}}\hspace{0.25in} (x,y,z \ne 0)$

6.3 Scientific Notation

Scientific notation is a convenient notation system used to represent large and small numbers. Examples of these are the mass of the sun or the mass of an electron in kilograms. Simplifying basic operations such as multiplication and division with these numbers requires using exponential properties.

Scientific notation has two parts: a number between one and nine and a power of ten, by which that number is multiplied.

$\text{Scientific notation: }a \times 10^b, \text{ where }1 \le a \le 9$

The exponent tells how many times to multiply by 10. Each multiple of 10 shifts the decimal point one place. To decide which direction to move the decimal (left or right), recall that positive exponents means there is big number (larger than ten) and negative exponents means there is a small number (less than one).

6.3 Examples/Practice

Write each number in scientific notation.

1.) 885.3

2.) 0.000744

3.) 1.09

4.) 0.039

5.) 15,000

Write each number in standard notation.

6.) 2.56 × 10²

7.) 9 × 10⁻⁴

8.) 5 × 10⁴

9.) 2 × 10⁰

Simplify each expression and write each answer in scientific notation.

10.) (2 × 10⁻⁶)(8.8 × 10⁻⁵)

11.) (5.1 × 10⁶)(9.84 × 10⁻¹)

12.) $\dfrac{(7.4 \times 10^4)(1.7 \times 10^{-4})}{(7.2 \times 10^{-1})(7.32 \times 10^{-1})}$