3 Geometry: Workbook Examples/Practice
Perimeter
Perimeter is a one-dimensional measurement that is taken around the outside of a closed geometric shape. Let’s start our discussion of the concept of perimeter with an example. If there are units, include units in your final result. Units will always be of single dimension (i.e. feet, inches, yards, centimeters, etc…)
Circumference
You may realize that we have not yet discussed the distance around a very important geometric shape: a circle! The distance around a circle has a special name called the circumference. To find the circumference of a circle, we use this formula: C = 2πr. π is a number in exact form. It is not rounded. 3.14 is a rounded form approximation for π.
Examples/Practice
1.) Find the perimeter of a square that has sides 14 inches long.
2.) Find the perimeter of a rectangle that is 5 yards by 28 yards.
3.) Find the perimeter of the shape below:
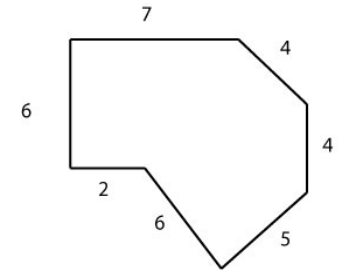
4.) Find the circumference of a circle with radius 7.5 inches.
5.) Find the circumference of a circle with diameter of 12 feet.
6.) Find the perimeter of a triangle with sides of length 3, 6, and 9 centimeters.
7.) Find the circumference of a circle with diameter 8.6 inches. Present answer in exact form and also compute using 3.14 for π. Present rounded form to the nearest tenth.
Finding Area
Area is a two-dimensional measurement that represents the amount of space inside a two-dimensional shape. To find the area, count the number of unit squares inside the shape. If there are units, include units in your final result. Units will always be two-dimensional (i.e. square feet, square yards, square miles, etc…). Note that you should not square the numerical answer that you calculated for area since the multiplication has already been completed. It is the units we must write as squared.
Examples/Practice
Find the area for each described situation. Create a drawing of the shape with the included information. Show all work. If units are included then units should be present in your final result. Use 3.14 for π and round answers to tenths as needed. Then repeat with using the Pi key on a calculator and compare answers.
1.) Find the area of a rectangle whose length is 8.4 meters and height is one-quarter that amount.
2.) Find the area of a triangle with base ![]() inches and height 5 inches.
inches and height 5 inches.
3.) Find the area of a circle with radius ![]() inches. Present answer in exact form and also compute rounded form using 3.14 for π. Present rounded form to the nearest tenth.
inches. Present answer in exact form and also compute rounded form using 3.14 for π. Present rounded form to the nearest tenth.
Similar Triangles
We can take information given about a relationship of two triangles to help get at an answer.
Similar triangles have the same angles and sides in proportion to each other. We can use that information to determine the height of something that we do not actually have the tools to measure. We can use the height of a person/object in relation to its shadow. To determine the height of the house, we set up a proportion.
Examples/Practice
1.) Mary was out in the yard one day and had her two daughters with her. She was doing some renovations and wanted to know how tall the house was. She noticed a shadow 5 feet long when her 5 foot, 3 inch tall daughter was standing 16 feet from the house. Draw a diagram to represent this then find the height of the house.
2.) Use the similar triangles process to determine the length of the missing sides. You may need to redraw your triangles to set up the proportions correctly.

3.) Mary (from the application that started this topic), decides to use what she knows about the height of the roof to measure the height of her second daughter. If her second daughter casts a shadow that is 1.5 feet long when she is 13.5 feet from the house, what is the height of the second daughter? Draw an accurate diagram and use similar triangles to solve.
Square Roots
Before we get to our last topic in this lesson—the Pythagorean Theorem,—we need to know a little bit about square roots.
- The square root of a number is that number which, when multiplied times itself, gives the original number. On your calculator, look for
 to compute square roots.
to compute square roots.  because 4 × 4 = 16
because 4 × 4 = 16 - A perfect square is a number whose square root is a whole number. The square root of a non-perfect square is a decimal value.
 is a perfect square.
is a perfect square. is not a perfect square.
is not a perfect square. - To obtain a decimal value for non-perfect square roots on your calculator, you may need to change the settings under your MODE button. Check your owner’s manual for help if needed.
 (rounded to hundredths)
(rounded to hundredths)
Examples/Practice
Find the square root of each of the following. Round to two decimal places if needed. Indicate those that are perfect squares and explain why.
1.) ![]()
2.) ![]()
3.) ![]()
The Pythagorean Theorem
The mathematician Pythagoras proved the Pythagorean theorem. The theorem states that given any right triangle with sides a, b, and c as below, the following relationship is always true: a2 + b2 = c2 a2 + b2 = c2
a2 + b2 = c2
Notes about the Pythagorean theorem:
- The triangle must be a right triangle (contains a 90º angle).
- The side c is called the hypotenuse and always sits across from the right angle.
- The lengths a and b are interchangeable in the theorem, but c cannot be interchanged with a or b. In other words, the location of c is very important and cannot be changed.
Example/Practice
1.) Use the Pythagorean theorem to find the missing hypotenuse length for a triangle with legs of 12 inches and 20 inches. Round to the tenths place.
2.) Use the Pythagorean theorem to find the missing side length for a triangle with hypotenuse 45 cm and leg of 24 cm. Round to the tenths place.
3.) In NBA Basketball, the width of the free-throw line is 12 feet.[1] A player stands at one exact corner of the free throw line (Player 1) and wants to throw a pass to his open teammate across the lane and close to the basket (Player 2). If his other teammate (Player 3—heavily guarded) is directly down the lane from him 16 feet, how far is his pass to the open teammate? Fill in the diagram below and use it to help you solve the problem.

Volume
Let’s revisit our friend Wally from “Area and Perimeter” in the textbook and use another aspect of his yard to introduce the concept of volume. Wally is a swimmer and wants to install a lap pool in his backyard. Because he has some extra space, he is going to build a pool that is 25 yards long, 2 yards wide, and 2 yards deep. How many cubic yards of water must be used to fill the pool (assuming right to the top).
Much as we did with area (counting unit squares), with volume we will be counting unit cubes. What is the volume of a unit cube? Let’s look at figure 1:
Finding the Volume of a Cube
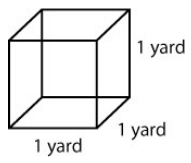
The shape at left is a cube (all sides are equal length). In particular, because all sides are of length 1, this cube is called a unit cube.
We know the area of the base from our previous work (1 yd × 1 yd or 1 square yard). We are going to take that area and extend it vertically through a height of 1 yard so our volume becomes
Volume = 1 yd × 1yd × yd = 1 cubic yard
Examples/Practice
1.) Filling Wally’s Pool How does this help Wally? Well, if he can count the number of unit cubes in his pool, he can determine the volume of water needed to fill the pool.

2.) Find the volume of each shape below.

3.) A box with sides of length 3 ft, 4 ft, ![]() ft.
ft.
Notes on Volume
- Volume is a three-dimensional measurement that represents the amount of space inside a closed three-dimensional shape.
- To find volume, count the number of unit cubes inside a given shape.
- If there are units, include units in your final result. Units will always be three-dimensional (i.e. cubic feet, cubic yards, cubic miles, etc…)
Volume of A Circular Cylinder
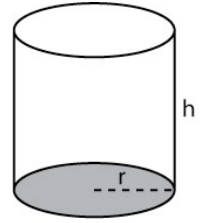
Can we use what we know about the area of a circle to formulate the volume of a can (also called a cylinder)? Take a look at figure 3.
The base circle is shaded. If we take the area of that circle (A = A = πr2) and extend it up through the height h, then our volume for the can would be:
V = πr2h.
Volume of Other Shapes
The chart below shows the volumes of some other basic geometric shapes.
| Shape | Volume |
|---|---|
| Sphere | |
| Cone | |
| Pyramid |
Examples/Practice
1.) Find the volume of the cylinder shown below.

2.) Find the volume of a sphere with radius 7 meters.
Determine the volume of each of the following. Include a drawing of the shape with the included information. Show all work. As in the examples, if units are included then units should be present in your final result. Use 3.14 for π and round answers to tenths as needed.
3.) Find the volume of a cube with side 5.3 meters.
4.) Find the volume of a box with sides of length 6 feet by ![]() feet by 9 feet.
feet by 9 feet.
5.) Find the volume of a can with radius 3.2 cm and height 8 cm.
6.) Find the volume of a sphere with diameter 11 yards.
7.) If you drank sodas from 5 cans each of diameter 4 inches and height 5 inches, how many cubic inches of soda did you drink? Use 3.14 for π and round to tenths.
Angles
Angles, often measured in degrees, measure the amount of rotation or “arc” between intersecting line segments. We need to have some sense of what an angle is before moving on to the next topic. See some examples and terminology below.
 |
|
 |
|
 |
|
 |
|
Surface Area
Nets: One final way to represent a solid is to use a net. If you cut out a net you can fold it into a model of a figure. Nets can also be used to analyze a single solid. Here is an example of a net for a cube.
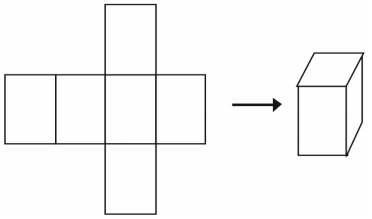
There is more than one way to make a net for a single figure.
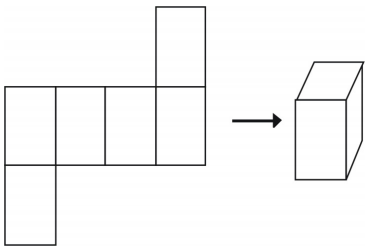
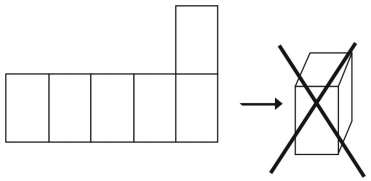
However, not all arrangements will create a cube.
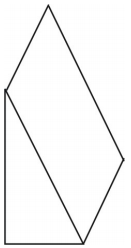
Example
What kind of net can you draw to represent the figure shown? Draw the net.
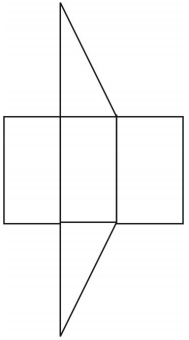
A net for the prism is shown. Other nets are possible.
Practice
Draw a net for each of the following:
1.) 
2.) 
Cylinders
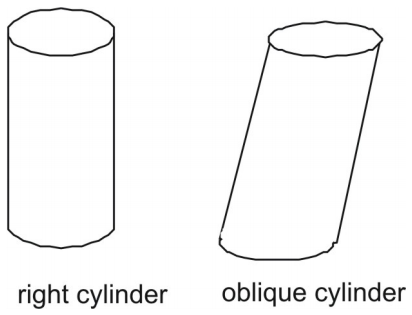
A cylinder is a three-dimensional figure with a pair of parallel and congruent circular ends, or bases. A cylinder has a single curved side that forms a rectangle when laid out flat.
As with prisms, cylinders can be right or oblique. The side of a right cylinder is perpendicular to its circular bases. The side of an oblique cylinder is not perpendicular to its bases.
Surface Area of a Cylinder Using Nets
You can deconstruct a cylinder into a net.
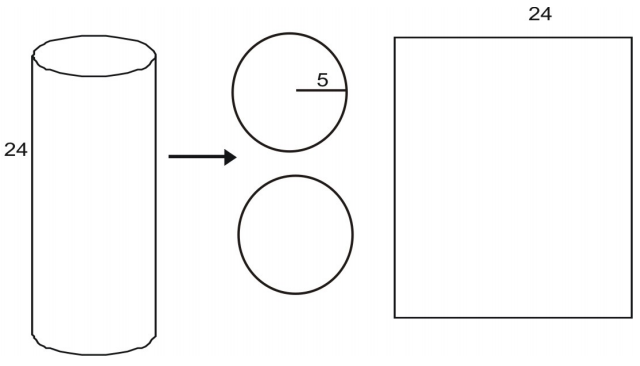
The area of each base is given by the area of a circle:
![]()
To find the width, imagine taking a can-like cylinder apart with a scissors. When you cut the lateral area, you see that it is equal to the circumference of the can’s top. The circumference of a circle is given by C = 2πr, the lateral area, L, is
![]()
Now we can find the area of the entire cylinder using A = (area of two bases) + (area of lateral side).
Area of a Right Cylinder: The surface area of a right cylinder, with radius and height h is given by A = 2B + L, where B is the area of each base of the cylinder and L is the lateral area of the cylinder.
More specifically,
The Surface Area of a Right Cylinder: A right cylinder with radius r and height h can be expressed as:
A = 2πr2 + 2πrh or: A = 2πr(r + h)
Examples/Practice
1.) Find the surface area of a right cylinder with radius 5 inches and height of 24 inches as in diagram above.
2.) Find the surface area of a right cylinder with diameter 32 cm and height of 7 cm.
3.) Challenge: Find the height of a cylinder that has radius 4cm and surface area of 226.08 sq cm.
Write the formula with the given information and solve for h.
![]()
Spheres
A sphere is a three-dimensional figure that has the shape of a ball.

Spheres can be characterized in three ways.
- A sphere is the set of all points that lie a fixed distance r from a single center point O.
- A sphere is the surface that results when a circle is rotated about any of its diameters.
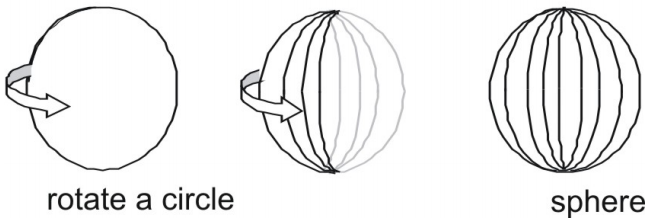
Surface Area of a Sphere
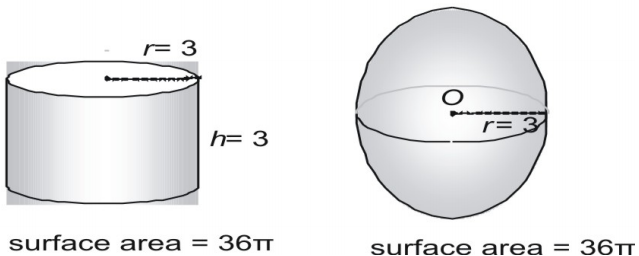
You can infer the formula for the surface area of a sphere by taking measurements of spheres and cylinders. Here we show a sphere with a radius of 3 and a right cylinder with both a radius and a height of 3 and express the area in terms of π.
Now try a larger pair, expressing the surface area in decimal form.
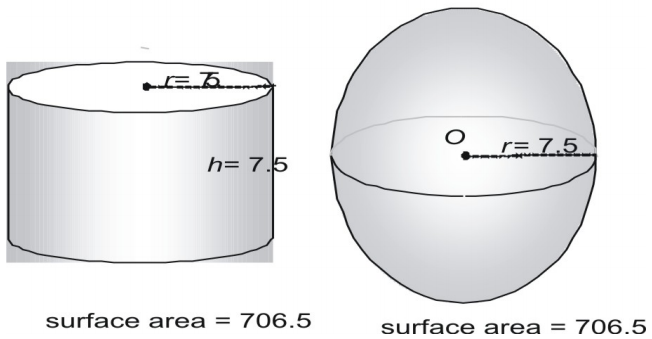
The Surface Area of a Sphere is given by: A = 4πr2
Examples/Practice
1.) Find the surface area of a sphere with a radius of 14 feet.
Use the formula.
![]()
2.) Find the radius of the sphere that has a volume of 335 cm3.
3.) Determine the surface area and volume of this shape with diameter 15:

4.) The radius of a sphere is 4. Find its volume and total surface area.
5.) A sphere has a radius of 5 inches. A right cylinder, having the same radius has the same volume. Find the height and total surface area of the cylinder.
6.) Sphere: volume = 296 cm3. Find the Diameter.
7.) Sphere: surface area is 179 in2. Find the Radius.
8.) Tennis balls with a diameter of 3.5 inches are sold in cans of three. The can is a cylinder. Assume the balls touch the can on the sides, top and bottom. What is the volume of the space not occupied by the tennis balls?
9.) A sphere has surface area of 36π in2. Find its volume.
10.) A giant scoop, operated by a crane, is in the shape of a hemisphere of radius = 21 inches. The scoop is filled with melted hot steel. When the steel is poured into a cylindrical storage tank that has a radius of 28 inches, the melted steel will rise to a height of how many inches?
- http://www.sportsknowhow.com ↵
