2 Solving Linear Equations: Workbook Examples/Practice
2.1 Solving Elementary Linear Equations
Solving linear equations is an important and fundamental skill in algebra. In algebra, there are often problems in which the answer is known, but the variable part of the problem is missing. To find this missing variable, it is necessary to follow a series of steps that result in the variable equaling some solution.
2.1 Examples/Practice
Solve each linear equation.
1.) ![]()
2.) ![]()
3.) ![]()
4.) ![]()
5.) ![]()
6.) ![]()
7.) ![]()
8.) ![]()
9.) ![]()
10.) ![]()
2.2 Solving Linear Equations
When working with questions that require two or more steps to solve, do the reverse of the order of operations to solve for the variable.
2.2 Examples/Practice
Solve each linear equation.
1.) ![]()
2.) ![]()
3.) ![]()
4.) ![]()
5.) ![]()
6.) ![]()
7.) ![]()
8.) ![]()
9.) ![]()
10.) ![]()
2.3 Solving Intermediate Linear Equations
When working with linear equations with parentheses, the first objective is to isolate the parentheses. Once isolated, the parentheses can be removed and then the variable solved.
When working with questions that require two or more steps to solve, do the reverse of the order of operations to solve for the variable.
2.3 Examples/Practice
Solve each linear equation.
1.) ![]()
2.) ![]()
3.) ![]()
4.) ![]()
5.) ![]()
6.) ![]()
7.) ![]()
8.) ![]()
9.) ![]()
10.) ![]()
11.) ![]()
12.) ![]()
4.1 Solving and Graphing Linear Inequalities
When given an equation, such as ![]() or
or ![]() there are specific values for the variable. However, with inequalities, there is a range of values for the variable rather than a defined value. To write the inequality, use the following notation and symbols:
there are specific values for the variable. However, with inequalities, there is a range of values for the variable rather than a defined value. To write the inequality, use the following notation and symbols:
| Symbol | Meaning |
|---|---|
| > Greater than | |
| ≤ Greater than or equal to | |
| < Less than | |
| ≥ Less than or equal to |
Key Take Away for Inequalities
When solving inequalities, the direction of the inequality sign (called the sense) can flip over. The sense will flip under two conditions:
First, the sense flips when the inequality is divided or multiplied by a negative. For instance, in reducing ![]() , it is necessary to divide both sides by −3. This leaves
, it is necessary to divide both sides by −3. This leaves ![]() >
> ![]()
Second, the sense will flip over if the entire equation is flipped over. For instance, ![]() >
> ![]() , when flipped over, would look like
, when flipped over, would look like ![]() In both cases, the 2 must be shown to be smaller than the
In both cases, the 2 must be shown to be smaller than the ![]() , or the
, or the ![]() is always greater than 2, no matter which side each term is on.
is always greater than 2, no matter which side each term is on.
4.1 Examples/Practice
Draw a graph for each inequality and give its interval notation.
1.) ![]() >
> ![]()
2.) ![]()
3.) ![]()
4.) ![]()
Write the inequality represented on each number line and give its interval notation.
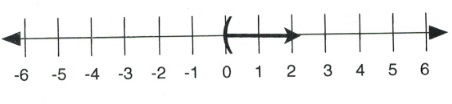
5.) 
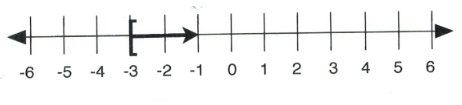
6.) 
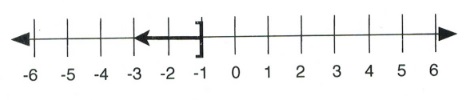
7.) 
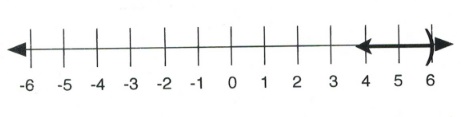
8.) 
Solve the inequality then draw a graph for each inequality and give its interval notation.
9.) ![]()
10.) ![]() >
> ![]()
11.) ![]()
12.) ![]()
4.5 Geometric Word Problems
It is common to run into geometry-based word problems that look at either the interior angles, perimeter, or area of shapes. When looking at interior angles, the sum of the angles of any polygon can be found by taking the number of sides, subtracting 2, and then multiplying the result by 180°.
Another common geometry word problem involves perimeter, or the distance around an object. For example, consider a rectangle, for which ![]()
4.5 Examples/Practice
Write the formula defining each relation. Do not solve.
1.) The length of a rectangle is 3 cm less than double the width, and the perimeter is 54 cm.
2.) The first angle of a triangle is twice as large as the second and 10° larger than the third.
3.) A 48 m piece of hose is to be cut into two pieces such that the second piece is 5 m longer than the first.
Write and solve the equation describing each relationship. Show all steps and interpret your answer in a sentence using appropriate units of measure and context.
4.) The second angle of a triangle is the same size as the first angle. The third angle is 12° larger than the first angle. How large are the angles?
5.) Two angles of a triangle are the same size. The third angle is 12° smaller than the first angle. Find the measure of the angles.
6.) Find the dimensions of a rectangle if the perimeter is 150 cm and the length is 15 cm greater than the width.
7.) If the perimeter of a rectangle is 304 cm and the length is 40 cm longer than the width, find the length and width.
8.) Find the length and width of a rectangular garden if the perimeter is 152 m and the width is 22 m less than the length.
9.) A lab technician cuts a 12 cm piece of tubing into two pieces such that one piece is two times longer than the other. How long are the pieces?
10.) An electrician cuts a 30 m piece of cable into two pieces. One piece is 2 m longer than the other. How long are the pieces?
