37 Practice: Linear Equations, Inequalities, & Geometric Word Problems (2.1 – 2.3; 4.1; 4.5) — Intermediate Algebra

Answer key in next section.

2.1 Solving Elementary Linear Equations

For questions 1 to 28, solve each linear equation.

  1. v + 9 = 16
  2. 14 = b + 3
  3. x - 11 = -16
  4. -14 = x - 18
  5. 30 = a + 20
  6. -1 + k = 5
  7. x - 7 = -26
  8. -13 + p = -19
  9. 13 = n - 5
  10. 22 = 16 + m
  11. 340 = -17x
  12. 4r = -28
  13. {-9} = \dfrac{n}{12}
  14. 27 = 9b
  15. 20v = -160
  16. -20x = -80
  17. 340 = 20n
  18. 12 = 8a
  19. 16x = 320
  20. 8k = -16
  21. -16 + n = -13
  22. -21 = x - 5
  23. p-8 = -21
  24. m - 4 = -13
  25. \dfrac{r}{14} = \dfrac{5}{14}
  26. \dfrac{n}{8} = {40}
  27. 20b = -200
  28. -\dfrac{1}{3} = \dfrac{x}{12}

2.2 Solving Linear Equations

For questions 1 to 20, solve each linear equation.

  1. 5 + \dfrac{n}{4} = 4
  2. -2 = -2m + 12
  3. 102 = -7r + 4
  4. 27 = 21 - 3x
  5. -8n + 3 = -77
  6. -4 - b = 8
  7. 0 = -6v
  8. -2 + \dfrac{x}{2} = 4
  9. -8 = \dfrac{x}{5} - 6
  10. -5 = \dfrac{a}{4} - 1
  11.  0 = -7 + \dfrac{k}{2}
  12. -6 = 15 + 3p
  13. -12 + 3x = 0
  14. -5m + 2 = 27
  15. \dfrac{b}{3} + 7 = 10
  16. \dfrac{x}{1} - 8 = -8
  17. 152 = 8n + 64
  18. -11 = -8 + \dfrac{v}{2}
  19. -16 = 8a + 64
  20. -2x - 3 = -29

2.3 Solving Intermediate Linear Equations

For questions 1 to 26, solve each linear equation.

  1. 2 - (-3a - 8) = 1
  2. 2(-3n + 8) = -20
  3. -5(-4 + 2v) = -50
  4. 2 - 8(-4 + 3x) = 34
  5. 66 = 6(6 + 5x)
  6. 32 = 2 - 5(-4n + 6)
  7. -2 + 2(8x -9) = -16
  8. -(3 - 5n) = 12
  9. -1 - 7m = -8m + 7
  10. 56p - 48 = 6p +2
  11. 1 - 12r = 29 - 8r
  12. 4 + 3x = -12x + 4
  13. 20 - 7b = -12b + 30
  14. -16n + 12 = 39 - 7n
  15. -2 - 5(2 - 4m) = 33 + 5m
  16. -25 - 7x = 6(2x - 1)
  17. -4n + 11 = 2(1 - 8n) + 3n
  18. -7(1 + b) = -5 - 5b
  19. -6v-29 = -4v - 5(v+1)
  20. -8(8r - 2) = 3r + 16
  21. 2(4x - 4) = -20 - 4x
  22. -8n - 19 = -2(8n - 3) + 3n
  23. -2(m - 2) + 7(m - 8) = -67
  24. 7 = 4(n - 7) + 5(7n + 7)
  25. 50 = 8(7 + 7r) - (4r + 6)
  26. -8(6 + 6x) + 4(-3 + 6x) = -12

4.1 Solving Linear Inequalities

For questions 1 to 6, draw a graph for each inequality and give its interval notation.

  1. n  > -5
  2. n  >  4
  3. -2 \le k
  4. 1 \ge k
  5. 5 \ge x
  6. -5 < x

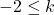
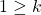
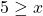
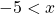
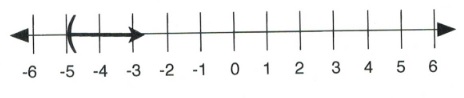
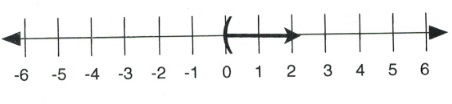
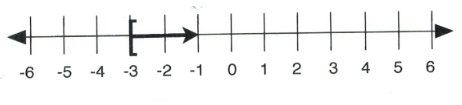
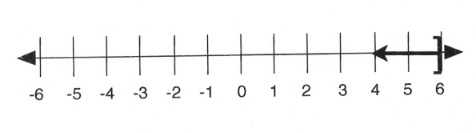
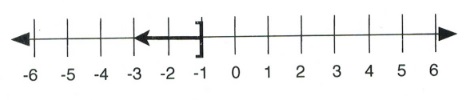
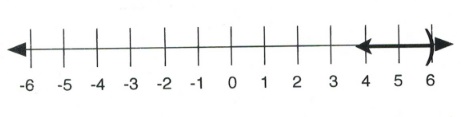
For questions 7 to 12, write the inequality represented on each number line and give its interval notation.

  1. image
  2. image
  3. image
  4. image
  5. image
  6. image

For questions 13 to 38, draw a graph for each inequality and give its interval notation.

  1. \dfrac{x}{11}\ge 10
  2. -2 \le \dfrac{n}{13}
  3. 2 + r < 3
  4. \dfrac{m}{5} \le -\dfrac{6}{5}
  5. 8+\dfrac{n}{3}\ge 6
  6. 11 > 8+\dfrac{x}{2}
  7. 2 > \dfrac{(a-2)}{5}
  8. \dfrac{(v-9)}{-4} \le 2
  9. -47 \ge 8 -5x
  10. \dfrac{(6+x)}{12} \le -1
  11. -2(3+k) < -44
  12. -7n-10 \ge 60
  13. 18 < -2(-8+p)
  14. 5 \ge \dfrac{x}{5} + 1
  15. 24 \ge -6(m - 6)
  16. -8(n - 5) \ge 0
  17. -r -5(r - 6) < -18
  18. -60 \ge -4( -6x - 3)
  19. 24 + 4b < 4(1 + 6b)
  20. -8(2 - 2n) \ge -16 + n
  21. -5v - 5 < -5(4v + 1)
  22. -36 + 6x > -8(x + 2) + 4x
  23. 4 + 2(a + 5) < -2( -a - 4)
  24. 3(n + 3) + 7(8 - 8n) < 5n + 5 + 2
  25. -(k - 2) > -k - 20
  26. -(4 - 5p) + 3 \ge -2(8 - 5p)

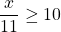
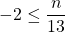
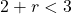
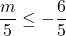
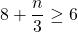
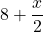
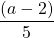
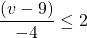
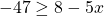
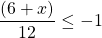
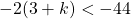
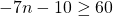
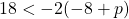
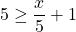
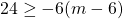
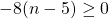
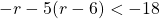
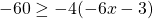
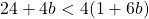
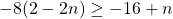
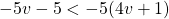
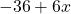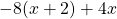
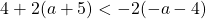
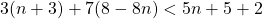
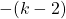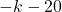
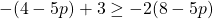
4.5 Geometric Word Problems

For questions 1 to 8, write the formula defining each relation. Do not solve.

  1. The length of a rectangle is 3 cm less than double the width, and the perimeter is 54 cm.
  2. The length of a rectangle is 8 cm less than double its width, and the perimeter is 64 cm.
  3. The length of a rectangle is 4 cm more than double its width, and the perimeter is 32 cm.
  4. The first angle of a triangle is twice as large as the second and 10° larger than the third.
  5. The first angle of a triangle is half as large as the second and 20° larger than the third.
  6. The sum of the first and second angles of a triangle is half the amount of the third angle.
  7. A 140 cm cable is cut into two pieces. The first piece is five times as long as the second.
  8. A 48 m piece of hose is to be cut into two pieces such that the second piece is 5 m longer than the first.

For questions 9 to 18, write and solve the equation describing each relationship.

  1. The second angle of a triangle is the same size as the first angle. The third angle is 12° larger than the first angle. How large are the angles?
  2. Two angles of a triangle are the same size. The third angle is 12° smaller than the first angle. Find the measure of the angles.
  3. Two angles of a triangle are the same size. The third angle is three times as large as the first. How large are the angles?
  4. The second angle of a triangle is twice as large as the first. The measure of the third angle is 20° greater than the first. How large are the angles?
  5. Find the dimensions of a rectangle if the perimeter is 150 cm and the length is 15 cm greater than the width.
  6. If the perimeter of a rectangle is 304 cm and the length is 40 cm longer than the width, find the length and width.
  7. Find the length and width of a rectangular garden if the perimeter is 152 m and the width is 22 m less than the length.
  8. If the perimeter of a rectangle is 280 m and the width is 26 m less than the length, find its length and width.
  9. A lab technician cuts a 12 cm piece of tubing into two pieces such that one piece is two times longer than the other. How long are the pieces?
  10. An electrician cuts a 30 m piece of cable into two pieces. One piece is 2 m longer than the other. How long are the pieces?

 

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Math in Society with Algebra Support Textbook Copyright © by jtrude is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book